Because the mean, standard deviation, and student scores are given, you use the formula:

to determine the z score for each scores. Then look up these z scores in a cumulative z score table, to find the probabilities associated with each of them. Subtract the lower probability from the higher probability and find the final answer.
For this problem:
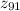
= 2.2 and
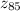
= 1.
The probabilities associated with these z scores are: 0.9861 and 0.8413 respectively. Therefore the probability that a randomly selected student scores between 85 and 90 = 0.9861 - 0.8413 = 0.1448 or 14.48 %
Jeff Negus
Tutoring In An Instant (TutIAI)