Question

Triangle QST is isosceles, and bisects T.

What is true about QRT? Check all that apply.

QRT = 90°
QRT = SRT
QRT STQ
QRT = 2*RTQ
QRT RTQ

Answer 1

The correct options are 1 and 2.

Explanation:

Given information: Triangle QST is isosceles, and bisects T.

In triangle QRT and SRT,

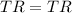`TR=TR` (common side)

`\angle STR=\angle QTR` (Bisector)

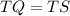`TQ=TS` (Isosceles triangle)

By SAS rule,

`\triangle STR\cong \triangle QTR`

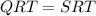`QRT=SRT` (CPCTC)

Bisector of an isosceles triangle is the altitude of triangle.

`\angle QRT=90^(\circ)`

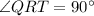
Therefore options 1 and 2 are correct.

Answer 2

Answer;

• QRT = 90°
• QRT = SRT

Explanation;

• An isosceles triangle is a type of triangle which has two sides equal, the base angles of this triangle are also equal or congruent.
• From the Isosceles triangle theorem, the perpendicular bisector of the base of an isosceles triangle also bisects the vertex angle. Thus, SR = RQ and ∠STR = ∠QTR .
• Thus; angle QRT is right angled, as TR acts as a perpendicular bisector of the base. Also SRT =QRT