Question

What is the sum of the first eight terms of the series?

(−800)+(−200)+(−50)+(−12.5)+...



Round the answer to two decimal places.

Answer 1

Observe that as the series progresses, the term decreases by 1/4. To show this, observe the first four terms of the series below.

-200 = (1/4)(-800)
-50 = (1/4)(-200)
-12.5 = (1/4)(-50)

Since we have a common ratio, r, of 1/4, we can use the properties of a geometric series to find the 8th term of the series.

Recall that to find the sum of the nth term of a geometric series, we have


`S_(n) = a((1-r^(n))/(1-r))`

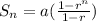
where a is the first term of the series and r is the ratio.

So, for the first eight terms, we have


`S_(8) = -800((1-((1)/(4))^8)/(1- (1)/(4)))`

`S_(8) \approx -1066.65`

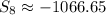
Therefore, the sum of the 8th series is approximately -1066.65.

Answer: -1066.65