Answer:
The piecewise function is given below as
![f(x)=\begin{cases}(x+3)^2+2;x\leq-2 \\ -2x+4,;-2<strong>Step 1:</strong><p>The first function is given below as</p>[tex]\begin{gathered} f(x)=(x+3)^2+2 \\ \text{when x=2} \\ f(2)=(-2+3)^2+2 \\ f(2)=1^2+2 \\ f(2)=1+2=3 \\ (-2,3) \end{gathered}]()
Hence, the graph above is a parabola that is opened upwards because the coefficient of the leading term is greater than 1, and it will be shaded at point (-2,3) because of the less than or equal to sign
(it has a negative slope that is as x-increase, y decreases, and vice versa)
Step 2:
The second function is given below as
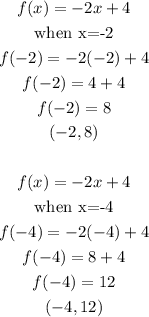
The second equation is a straight line that will be open at points (-2,8) and (4,12) because of the strictly less than sign
Step 3:
The thrid function is
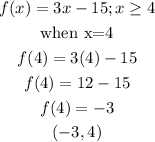
The equation above is a straight line and will be shaded at point (-3,4) because of the greater than or equal to sign
(it has a positive slope that is as x increases,y also increases and vice versa)
Hence,
The final answer will be