Question

The diagonal of a TV is 26 inches long. Assuming that this diagonal forms a pair of 30-60-90 right triangles, what are the exact length and width of the TV? A. 13 inches by 13√3 B. 13√2 inches by 13√2 inches C. 52√2 inches by 52√2 inches D. 52 inches by 52√3 inches

Answer 1

Let

x-------> the length side of the TV

y-------> the width of the TV

d------> the diagonal of a TV

we know that

in a 30-60-90 right triangle

`cos(30\°)=(√(3))/(2)\\\\sin(30\°)=(1)/(2)`

`d=26\ in`

`sin(30\°)=(y)/(d)` ---->
`y=d*sin(30\°)`

`cos(30\°)=(x)/(d)` ---->
`x=d*cos(30\°)`

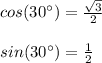
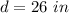
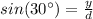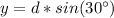
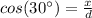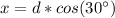
substitute the values

`y=26*(1)/(2)=13\ in`

`x=26*(√(3))/(2)=13√(3)\ in`

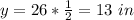
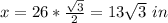
the length side of the TV is
`13√(3)\ in`

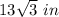
the width of the TV is
`13\ in`

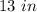
therefore

the answer is the option A

13 inches by 13√3 inches