Let's draw the given coordinates on a Cartesian plane:
The above figure seems to be a rectangle. However, we need to check if the interior angles measure 90 degrees. We can check it by finding the slopes of the respective lines. For instance, the slope of the line betwwen point T and S is

and the line between point T and V is

Then, those lines are perpendicular if M is the negative reciprocal of m, that is,

Then, by substituting the above results, we have
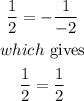
Then, the lines are perpendicular each other.
Simiarly, we need to check the same for lines SR and VR, that is,
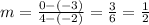
and
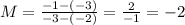
So, we can corroborate that

because
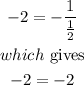
Therefore, the figure is a rectangle.