Question

Which of the following is true about the sequence graphed below?

A. The sequence is arithmetic because the terms have a common difference.
B. The sequence is arithmetic because the terms do not have a common difference.
C. The sequence is not arithmetic because the terms have a common difference.
D. The sequence is not arithmetic because the terms do not have a common difference.

Answer 1

a, because it declines at a steady ratw

Answer 2

Answer with explanation:

When you will look, at the points in the coordinate plane, (2,9), (3, 7.5), (4,6), (5,4.5), (6,3), (7,1.5), (8,0), they lie along a straight line, because

Slope between two points

`=(9-7.5)/(2-3)=(7.5-6)/(3-4)=(4.5 -3)/(5-6)=(3-1.5)/(6-7)=(1.5-0)/(7-8)\\\\=-1.5`

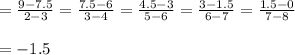
So,all the points lie in a line.

y(0)=8

y(1.5)=7

y(3)=6

y(4.5)=5

y(6)=4

y(7.5)=3

y(9)=2

Now ,difference between two consecutive terms = 7-8=6-7=5-6=4-5=3-4=2-3=-1

So,→ Sequence is Arithmetic, because the terms have a common Difference.

Option A