Question

A ball is thrown into the air with an upward velocity of 32 ft/s. Its height h in feet after t seconds is given by the function h = –16t2 + 32t + 6. a. In how many seconds does the ball reach its maximum height? Round to the nearest hundredth if necessary. b. What is the ball’s maximum height?

A. 1 s; 22 ft

B. 2 s; 22 ft

C. 1 s; 54 ft

D. 2 s; 6 ft

Answer 1

The max is -b/2a so find -b/2a then sub into the equation it looks like it is a

Answer 2

A. 1 second ; 22 ft

Explanation:

We have been given that a ball is thrown into the air with an upward velocity of 32 ft/s. Its height h in feet after t seconds is given by the function
`h=-16t^2+32t+6`.

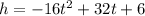a. To find the time it will take the ball to reach its maximum height, we need to find x-coordinate of vertex of our given parabola.

We will use
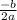`(-b)/(2a)` to find the x-coordinate of vertex of our given parabola.

`(-32)/(2* -16)`

`(-2)/(-2)=1`

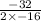
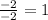
Therefore, the ball will reach its maximum after 1 second.

b. To find the ball's maximum height we need to evaluate our given equation at
`t=1`.

`h=-16(1)^2+32(1)+6`

`h=-16*1+32+6`

`h=-16+32+6`

`h=22`

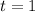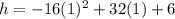
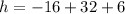
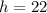
Therefore, the maximum height of ball is 22 ft.

Upon looking at our given choices we can see that option A is the correct choice.