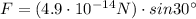Question

One beam of electrons moves at right angles to a magnetic field. The force on these electrons is 4.9 × 10-14 newtons. A second beam travels at the same speed, but at a 30° angle with the magnetic field. What force is on these electrons?

A.(4.9 × 10-14 newtons) · tan(30°)
B.(4.9 × 10-14 newtons) · sin(30°)
C.(4.9 × 10-14 newtons) · cos(30°)
D.(4.9 × 10-14 newtons) · arctan(30°)
E.(4.9 × 10-14 newtons) · arccos(30°)

Answer 1

Force on a particle with charge q moving with velocity v at an angle θ to a magnetic field B is F=qvBsin(θ).  So B is correct

Answer 2

B.(4.9 × 10-14 newtons) · sin(30°)

Step-by-step explanation:

The magnetic force exerted on charged particles by a magnetic field is given by

`F=qvB sin \theta`

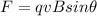
where

q is the charge

v is the speed of the charge

B is the magnetic field intensity

`\theta` is the angle between the direction of v and B

The first beam moves at right angle to the magnetic field, so
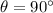`\theta=90^(\circ)` and the force on this beam is simply

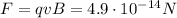`F=qvB=4.9\cdot 10^(-14) N` (1)

The second beam moves at angle of
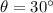`\theta=30^(\circ)`. The electrons are travelling at same speed v, and the magnetic field is still the same (and the charge q is also the same, since they are electrons as well), so the magnetic force in this case is

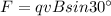`F=qvB sin 30^(\circ)` (2)

But from the previous equation we know that

`qvB = 4.9\cdot 10^(-14) N`

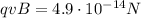
so, if we substitute into eq. (2), we find

`F=(4.9\cdot 10^(-14) N) \cdot sin 30^(\circ)`