Answer:
22883$
Explanation:
We can use the concept of compound interest. Compound interest is the benefit of an investment at an interest rate over a certain period of time. The formula for compound interest is:
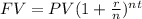
Where:

Using the data provided by the problem:

Therefore:
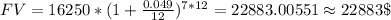
Hence, the value of the investment after 7 years is 22883$