Given the table:
x y
0 0
1.3 3.9
5 15
8 24
Let's find the function equation for the input/output table.
Apply the slop-intercept form:
y = mx + b
Where m is the slope and b is the y-intercept.
To find the slope, apply the slope formula:
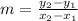
Take two points from the table:
(x1, y1) ==> (0, 0)
(x2, y2) ==> (5, 15)
We have:
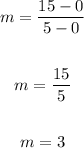
The slope, m = 3
The y-intercept is the point, the line crosses the y-axis. At this point the x-coordinate is 0.
From the table, when x = 0, y = 0
Therefore, the y-intercept is at y = 0.
Hence, the function equation for the input/output table is:
y = 3x + 0
y = 3x
ANSWER:
y = 3x