Question

If the circle x2 - 4x + y2 + 2y = 4 is translated 3 units to the right and 1 unit down, what is the center of the circle?

Answer 1

The equation of a circle with center at (a,b) and radius r is: (x-a)^2+(y-b)^2=r^2.

This circle has been translated from (0,0) to (a,b).

The equation of the circle in our case can be rewritten as: (x-2)^2+(y-2)^2=2^2

Moving the graph 3 units to the right is: (x-2-3)^2+(y-2)^2=2^2.

Moving the graph 1 unit down is: (x-2-3)^2+(y-2-1)^2=2^2.

This gives the equation: (x-5)^2+(y-3)^2=2^2

So, the center of the circle is: (5,3)

Answer 2

Answer: The new co-ordinates of the center are (5, -2).

Step-by-step explanation: The given equation of a circle is

`x^2-4x+y^2+2y=4~~~~~~~~~~~~~~~~~~~~~~~~(i)`

We are to find the center of the above circle if the circle (i) is translated 3 units to the right and 1 unit down.

The standard equation of a circle with radius r units and center at (h, k) is given by

`(x-h)^2+(y-k)^2=r^2.`

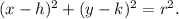
From equation (i), we have

`x^2-4x+y^2+2y=4\\\\\Rightarrow (x^2-4x+4)+(y^2+2y+1)-4-1=4\\\\\Rightarrow (x-2)^2+(y+1)^2=9\\\\\Rightarrow (x-2)^2+(y+1)^2=3^2.`

Comparing the above equation with the standard equation of a circle, we get

center, (h, k) = (2, -1) and radius, r = 3 units.

If the circle is translated 3 units to the right and 1 unit down, then the co-ordinates of the new center will be

(h', k') = (h+3, k-1) = (2+3, -1-1) = (5, -2).

Thus, the new co-ordinates of the center are (5, -2).