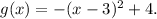Question

The parent function f(x) = x2 is translated such that the function g(x) = –x2 + 6x – 5 represents the new function. What is true about the transformation that was performed?

Answer 1

a c d

Explanation:

Answer 2

1. Translation 3 units to the right;

2. Reflection across the x-axis;

3. Translation 4 units up.

Explanation:

First, rewrite the function
`g(x)` in following way:

`g(x)=-x^2+6x-5=-(x^2-6x)-5=-(x^2-6x+9-9)-5=-(x-3)^2+9-5=-(x-3)^2+4.`

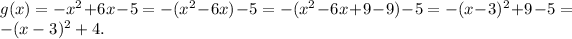
Apply such transformations:

1. Translate the graph of the parent function
`f(x)` 3 units to the right to get the graph of the function
`f_1(x)=(x-3)^2.`

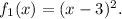
2. Reflect the graph of the function
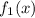`f_1(x)` across the x-axis to get the graph of the function
`f_2(x)=-(x-3)^2.`

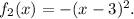
3. Translate the graph of the function
`f_2(x)` 4 units up to get the graph of the function
`g(x)=-(x-3)^2+4.`