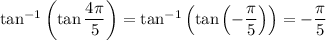This is because
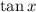
is a multivalued function and is not invertible over its entire domain. We restrict its domain to the interval

, which gives one complete branch of values (or one period).
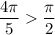
and thus

is outside the domain.
A different way to go about this is to find the value of
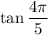
first, then compute the inverse tangent of that result. But finding the trigonometric values of multiples of
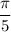
is somewhat tricky and perhaps more work than is needed.
Instead, we can use a trigonometric identity to find the value of
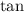
whenever its argument falls outside the "standard" branch.
We know that

(because
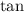
is

-periodic), so
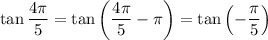
. And now the function can be inverted, so that