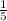Question

What is the scale factor of ABC to XYZ?

Answer 1

Option C is correct.

`(1)/(5)`

Explanation:

Scale factor is defined as the ratio of the image

In triangle ABC and triangle XYZ:

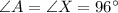`\angle A = \angle X = 96^(\circ)` [Angle]

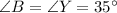`\angle B = \angle Y = 35^(\circ)` [Angle]

AA similarity states that the two triangles have the corresponding angles that are equal in measure.

by AA similarity we have;

Triangle ABC and triangle XYZ are similar.

Then by definition of similar triangles:

Corresponding sides are in proportion:

`(AB)/(XY)=(BC)/(YZ) = (AC)/(XZ)`

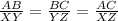
Scale factor: The reduced ratio of two corresponding sides of a given triangles.

then;

`(AB)/(XY) = (1)/(k)`

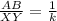
Substitute the given values:

`(45)/(9) = (1)/(k)`

Simplify

`(1)/(k) =5`

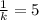
or

`k = (1)/(5)`

Therefore, the scale factor of triangle ABC to triangle XYZ is:
`(1)/(5)`

Answer 2

we know that

Triangles ABC and XYZ are similar

so

The ratio of the corresponding sides are equal, and this ratio is called the scale factor

`(XY)/(AB)= (YZ)/(BC)= (XZ)/(AC)`

substitute the values

`(9)/(45)= (12)/(60)= (7)/(35)= (1)/(5)`

therefore

the answer is the option C

`(1)/(5)`