Question

Help with test review to study for final next week.

Answer 1

The exponential decay is given by:

`A=A_0e^(rt)`

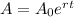
where A0 is the initial amount of the element and r is the decay rate.

To find the decay rate we use the fact that the half life is 1590 years; this means that it takes 1590 years for the amount of substance to be half the original amount, that is:

`(1)/(2)A_0=A^{}_0e^(1590r)`

Solving for r we have:

`\begin{gathered} (1)/(2)A_0=A^{}_0e^(1590r) \\ (1)/(2)=e^(1590r) \\ \ln (1)/(2)=\ln (e^(1590r)) \\ \ln (1)/(2)=1590r \\ r=(1)/(1590)\ln (1)/(2) \end{gathered}`

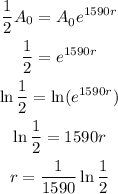
Hence the decay rate is:

`r=(1)/(1590)\ln (1)/(2)`

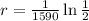
Now that we have the decay rate we have that the function describing the amount of radium for our example is:

`A=100e^{((1)/(1590)\ln (1)/(2))t}`

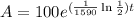
To determine how much radium we have after 1000 years we plug t=1000 in the function above:

`\begin{gathered} A=100e^{((1)/(1590)\ln (1)/(2))(1000)} \\ A=64.67 \end{gathered}`

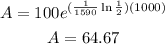
Therefore after 1000 years we have 64.67 mg of radium-226