Conditional probability is the probability that an event is occurring while another has occured. Mathematically, we can compute for the conditional probability, P(A|B) as
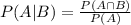
where P(A∩B) is the probability that events A AND B are occurring at the same time and P(A) is the probability for A to happen.
For our case, given that 50% of the bags contain red, 25% contain pink, and 15% contains red & pink. Thus, we have
P(R) = 0.50
P(P) = 0.25
P(R∩P) = 0.15
So, the conditional probability of the events below to happen can be calculated as shown.
1.
conditional probability that a bag of pink candy also contains red candy is
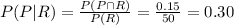
2. conditional probability that a bag of red candy also contains pink candy is
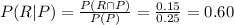
From this, we see that the conditional probability that a bag of red candy also contains pink candy is greater.