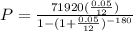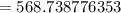Question

Jamie purchased a condo for $89,900 with a down payment of 20%; her credit terms were 5% for 15 years. what is jamie's monthly payment?

Answer 1

`\bf \qquad \qquad \textit{Amortized Loan Value} \\\\ pymt=P\left[ \cfrac{(r)/(n)}{1-\left( 1+ (r)/(n)\right)^(-nt)} \right] \\\\`


`\bf \begin{cases} P= \begin{array}{llll} \textit{original amount}\\ \end{array}\to & \begin{array}{llll} \quad89900\\ \ \ -20\%\\ -17980\\ -----\\ \quad 71920 \end{array}\\ pymt=\textit{periodic payments}\\ r=rate\to 5\%\to (5)/(100)\to &0.05\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{payments are monthly, thus} \end{array}\to &12\\ t=years\to &15 \end{cases} \\\\\\ pymt=71920\left[ \cfrac{(0.05)/(12)}{1-\left( 1+ (0.05)/(12)\right)^(-12\cdot 15)} \right]`

Answer 2

$ 568.74 ( approx )

Explanation:

Since, the monthly payment formula is,

`P=(PV(r))/(1-(1+r)^(-n))`

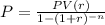
Where,

PV = present value of the loan or borrowed amount,

r = monthly rate,

n = number of months,

Given,

The value of condo = $ 89,900,

Down payment rate = 20%,

Thus, the borrowed amount, PV = 89900 - 20% of 89900

`=89900-(20* 89900)/(100)`

`=89900-17980`

`=\$71920`

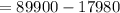
APR = 5% = 0.05 ⇒ r =
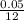`(0.05)/(12)` ( 1 year = 12 months ),

Time = 15 years ⇒ n = 15 × 12 = 180

Hence, the monthly payment would be,

`P=(71920((0.05)/(12)))/(1-(1+(0.05)/(12))^(-180))`

`=568.738776353`

`\approx \$ 568.74`