Question

Between x = 0 and x = 1, which function has a smaller average rate of change than y = 3x ? A) y = 8x + 2 B) y = 3x + 2 Eliminate C) y = 2x

Answer 1

The average rate of change of a function over a closed interval [a,b] is given with : f(b)-f(a)/(b-a).

The interval in our case is [0,1]. The average rate of change fot the function y=3x is:

(3*1-3*0)/(1-0)=3/1=3

We will calculate the average rate of changes of all listed functions:

A) y = 8x + 2

(8*1+2) – (8*0+2)/(1-0)=(10-2)/1=8/1=8

B) y = 3x + 2

(3*1+2) – (3*0+2)/1=5-2=3

C) y = 2x

(2*1) – (2*0)/1=2

So, smaller average rate of change has the function y=2x.

Answer 2

option C has smallest rate of change

Explanation:

given points x = 0 and x = 1

hence putting value in equation y = 3x

y = 0 and y = 3

rate of change of =
`(y_2-y_1)/(x_2-x_1)=(3-0)/(1-0) = 3`

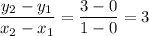
from equation A) y = 8 x + 2

at x = 0 y = 2 and at x = 1 y = 10

rate of change =
`(y_2-y_1)/(x_2-x_1)=(10-2)/(1-0) =8`

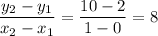
B) y = 3 x + 2

at x = 0 y = 2 and at x = 1 y = 5

rate of change =
`(y_2-y_1)/(x_2-x_1)=(5-2)/(1-0) =3`

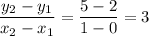
C) y = 2 x

at x = 0 y = 0 and at x = 1 y = 2

rate of change =
`(y_2-y_1)/(x_2-x_1)=(2-0)/(1-0) =2`

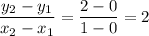
hence, option C has smallest rate of change