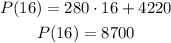ANSWER
The formula is P(t) = 280t + 4220
In 2006 the population will be 8700
Step-by-step explanation
If the population changes linearly, we're looking for a formula like:
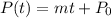
P0 is the initial population, in 1990. m is the slope and t is the time in years since 1990.
We have two points (t, P(t)):
• (1, 4500) --> 1 year after 1990 the population was 4500
,
• (6, 5900) --> 6 years after 1990 the population was 5900.
With this information we can find the slope m:
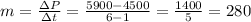
The slope is 280. For now, the formula is:
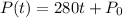
To find the y-intercept P0, we have to use one of the points. Using the first point (1, 4500) replace P(t) = 4500 and t = 1 and solve for P0:
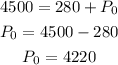
The formula is:
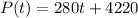
To find the population in 2006 we have to know how many years after 1990 is 2006:
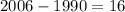
We have to replace t = 16 in our formula: