Question

Erica plotted the three towns closest to her house on a graph with town AA at (9, 12), town BB at (9, 7) and town CC at (1, 1). She drew the triangle joining the 3 points. Which lists the angles formed in size, smallest to largest?

Answer 1

To compute the distance between the points, we can apply the distance formula as shown below.


`d = \sqrt{(x_(1) - x_(2))^(2) + (y_(1) - y_(2))^(2) }`

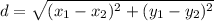
In which x₁ and x₂ are the x-coordinates and y₁ and y₂ are the y-coordinates of the two points. Thus, applying this with the segments AABB, AACC, and BBCC, we have


`\overline{AABB} = \sqrt{(9-9)^(2) + (12-7)^(2)} = 5`

`\overline{AACC} = \sqrt{(9-1)^(2) + (12-1)^(2)} = √(185)`

`\overline{BBCC} = \sqrt{(9-1)^(2) + (7-1)^(2)} = 10`

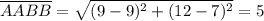
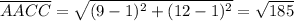
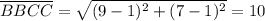
Now that we have the lengths of all the sides of ΔAABBCC, we can find the missing angles using the Law of Cosines.

Generally, we have


`c^(2) = a^(2) + b^(2) - 2abcosC`

or


`C = cos^(-1) ((a^(2) + b^(2) - c^(2))/(2ab))`

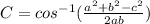
Hence, we have


`\angle AA = cos^(-1) (((√(185))^(2) + 5^(2) - 10^(2))/(2(5)(\sqrt185)))`

`\angle BB= cos^(-1) ((5^(2) + 10^(2) - (√(185))^(2))/(2(5)(10)))`

`\angle CC= cos^(-1) ((10^(2) + (√(185))^(2) - 5^(2))/(2(5)(√(185))))`

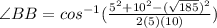
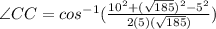
Simplifying this, we have


`\angle AA = 36.03^(0)`

`\angle BB = 126.87^(0)`

`\angle CC = 17.10^(0)`

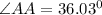
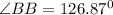
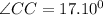
Thus, from this, we can arrange the angles from smallest to largest: ∠CC, ∠AA, and ∠BB.

Answer: ∠CC, ∠AA, and ∠BB