Answer:
 is the probability that the first student chosen will be a girl and the second will be a boy.
is the probability that the first student chosen will be a girl and the second will be a boy.
Explanation:
we are given the following information in the question:
Total number of students in a class = 9
Total number of girls in a class = 5
Total number of boys in a class = 4
We have to find the probability that the first student chosen will be a girl and the second will be a boy.
Formula:
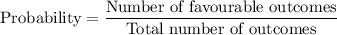
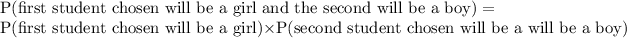
Working:

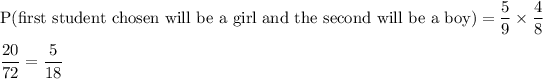
Hence,
 is the probability that the first student chosen will be a girl and the second will be a boy.
is the probability that the first student chosen will be a girl and the second will be a boy.