Given,
The weight of the box, W=300 N
The coefficient of static friction, μ=0.30
(a) In order to move the box, the force applied must be greater than the static friction that exists between the box and the floor. The static friction is given by,
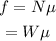
Where N is the normal force which is the same as the weight of the box.
On substituting the known values,
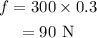
Thus the horizontal force required to start the box into motion is 90 N.
(b) The applied force is F= 50.0 N
The coefficient of kinetic friction μ=0.3
Thus, the kinetic friction offered by the floor is,
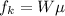
On substituting the known values,
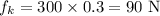
Thus the net force acting on the body will be,
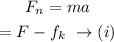
Where m is the mass of the box and a is the acceleration of the box
The mass is given by
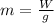
Where g is the acceleration due to gravity.
On substituting the known values,
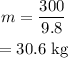
Thus, from equation (i) the acceleration is calculated as
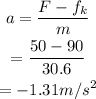
Thus the acceleration of the box will be -1.31 m/s². The negative sign indicates that it is a deceleration. Thus, the box will eventually slow down and will come to rest.