Question

Question 7 please. Asking for what horizontal force is necessary to start the box into motion

Answer 1

Given,

The weight of the box, W=300 N

The coefficient of static friction, μ=0.30

(a) In order to move the box, the force applied must be greater than the static friction that exists between the box and the floor. The static friction is given by,

`\begin{gathered} f=N\mu \\ =W\mu \end{gathered}`

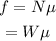
Where N is the normal force which is the same as the weight of the box.

On substituting the known values,

`\begin{gathered} f=300*0.3 \\ =90\text{ N} \end{gathered}`

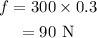
Thus the horizontal force required to start the box into motion is 90 N.

(b) The applied force is F= 50.0 N

The coefficient of kinetic friction μ=0.3

Thus, the kinetic friction offered by the floor is,

`f_k=W\mu`

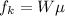
On substituting the known values,

`f_k=300*0.3=90\text{ N}`

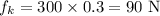
Thus the net force acting on the body will be,

`\begin{gathered} F_n=ma \\ =F-f_k\text{ }\rightarrow(i) \end{gathered}`

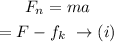
Where m is the mass of the box and a is the acceleration of the box

The mass is given by

`m=(W)/(g)`

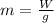
Where g is the acceleration due to gravity.

On substituting the known values,

`\begin{gathered} m=(300)/(9.8) \\ =30.6\text{ kg} \end{gathered}`

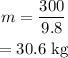
Thus, from equation (i) the acceleration is calculated as

`\begin{gathered} a=(F-f_k)/(m) \\ =(50-90)/(30.6) \\ =-1.31m/s^2 \end{gathered}`

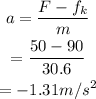
Thus the acceleration of the box will be -1.31 m/s². The negative sign indicates that it is a deceleration. Thus, the box will eventually slow down and will come to rest.