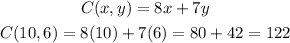Question

1. Daniel works no more than 16 hours a week while attending college. He wants to spend at least 2 hours but no more than 10 hours a week parking cars. He is paid $8 per hour parking cars (x) and $7 per hour working at the Haul-Mart store (y). What are Daniel's maximum earnings? a) Define the variables. b) What are the constraints? c) What is the cost function? C(x,y) =

Answer 1

a.

Let:

M = maximum number of hours that Daniel can work per week

x = Number of hours spend a week parking cars

y = Number of hours spend working at the Haul- Mart store

C(x,y) = Maximum earnings.

b. Daniel works no more than 16 hours a week while attending college, Therefore:

`x+y\leq16`

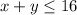
He wants to spend at least 2 hours but no more than 10 hours a week parking cars, hence:

`\begin{gathered} x\ge2;x\leq10 \\ or \\ 2\leq x\leq10 \end{gathered}`

c. He is paid $8 per hour parking cars (x) and $7 per hour working at the Haul-Mart store (y):

`C(x,y)=8x+7y`

-------------------------------------------------

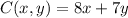
the maximum number of hours he wants to work in the parking lot is 10, so:

`\begin{gathered} x+y\leq16 \\ \text{If x=10} \\ 10+y\leq16 \\ \text{Solving for y:} \\ y\leq16-10 \\ y\leq6 \end{gathered}`

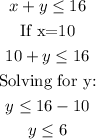
Replacing those values into the cost function:

`\begin{gathered} C(x,y)=8x+7y \\ C(10,6)=8(10)+7(6)=80+42=122 \end{gathered}`