Question

A baseball player hit a ball with an upward velocity of 46 ft/s. Its height in feet after t seconds is given by the function h= -16t^2+46t+6. What is the maximum height the ball reaches? How long will it take to reach maximum height? How long does it take to hit the ground?

Answer 1

maximum height: h=39.06 ft

time for the ball to reach its maximum height: t= 1.4375 s

time it takes for the ball to touch the ground:
`t_(g)  = 2 * 1.4375 = 2.875s`

Explanation:

The function h (t) has a maximum value when h´(t) = 0

h´(t) is the derivative of h with respect to t.

We find h´(t)) to calculate the time for the ball to reach its maximum height

h = -16t²+ 46t + 6 Equation (1)

h´(t) = -32t + 46

-32t + 46 = 0

46 = 32t

t = 46/32 = 1.4375 s

We replace 1.4375 s in equation (1) to calculate the maximum height:

h = -16 (1.4375) ² + 46 (1.4375) + 6

h = 39.06 ft

The time it takes for the ball to touch the ground (
`t_(g)`) is twice the time it takes to reach the maximum height.

`t_(g) =2t`

`t_(g)  = 2 * 1.4375 = 2.875s`

Answer 2

Given the function h(t) where t is the time, to find the maximum height reached by the ball, we must find the maximum value of h(t) = -16t² + 46t + 6. Since h(t) is a quadratic function, to find its maximum value, we need to look for the coordinates of its vertex (x, y). To solve for the x-coordinate, we have


`x = (-b)/(2a)`

`x = (-46)/(2(-16)) = (23)/(16)`

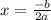
Thus, it takes t = 23/16 s for the ball to reach the maximum height. To find the maximum height, we need to substitute the value of t into h(t).

h = -16(23/16)² + 46(23/16) + 6
h = 625/16 ft

For the ball to reach ground level, then h must be equal to zero. Thus, we have

0 = -16t² + 46t + 6
0 = 4t² - 23t - 3

Recalling the quadratic formula, we have


`t = \frac{-b \pm \sqrt{b^(2)-4ac} }{2a}`

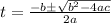
where a , b, and c are the coefficients of the quadratic equation. For our case, a = 4, b = -23, and c = -3. Thus, we have


`t = \frac{23 \pm \sqrt{23^(2)-4(4)(-23)} }{2(4)}`

`t = (23 \pm √(897))/(8)`

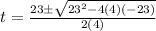
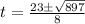
Since time cannot be negative, we disregard the negative root and have t = (23 + √897)/8 s.

Answer:
Maximum time = 23/16 seconds
Maximum height = 625/16 ft
Time taken to reach the ground = (23 + √897)/8 seconds