We have the following information about the two companies:
Pro Painters:
• They charge $200 per hour
• They charge a fixed cost of $6000 in material fees.
Illusion Ltd:
• They charge $150 per hour
• They charge a fixed cost of $8000 in material fees.
Finding the equations that model the cost
And we have to find an equation that models the cost of using each company, where C represents the cost in dollars, and h is the number of hours.
1. To find each equation, we can notice that both cases can be represented as a linear function, since the cost in each case is constant, $200 per hour, using Pro Painters, and $150 per hour, using Illusion Ltd. They are the slope of a line in both cases.
2. We can also notice that $6000 is the y-intercept for the linear function (Pro Painters), and $8000 is the y-intercept for Illusion Ltd. The y-intercept is a point where the line passes through the y-axis and at this point x = 0.
3. Therefore, we can model the cost for each company as follows:
Pro Painters

Illusion Ltd
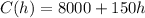
Hence, we have:
• Pro Painters: C(h) = 6000 + 200h
• Illusion Ltd: C(h) = 8000 + 150h
Determining when the two companies will charge the same price for painting and how much it will cost
1. To determine the same price, we need to equal both equations as follows:

2. Now, to solve the equation, we can subtract 150h from both sides of the equation:
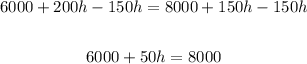
Now, we can subtract 6000 from both sides, and then divide by 50 as follows:
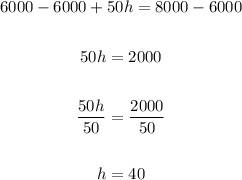
Therefore, the two companies charge the same price for painting at the 40 hours, and the cost will be:
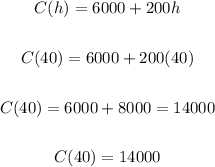
If we use the other equation, C(h) = 8000 + 150h, we will get the same answer.
Therefore, the cost will be $14000 for both companies.
Hence, in summary, we have:
Equations that model the cost for using each company:
• Pro Painters: C(h) = 6000 + 200h
• Illusion Ltd: C(h) = 8000 + 150h
The two companies will charge the same price for the 40 hours, and the cost will be $14,000.