Question

A large software company gives job applicants a test of programming ability and the mean for that test has been 160 in the past. twenty-five job applicants are randomly selected from one large university and they produce a mean score and standard deviation of 183 and 12, respectively. use a 0.05 level of significance to test the claim that this sample comes from a population with a mean score greater than 160.

Answer 1

See attachment for answer.

Answer 2

Explanation:

Mean of the test of programming ability was 160 in the past.

Again now, twenty-five job applicants are randomly selected from one university and they produce a mean score and standard deviation of 183 and 12.

So in this case, the null hypothesis will be,

`H_o: \mu = 160`

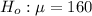
and alternate hypothesis will be,

`H_a: \mu > 160`

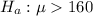
Mean of the sample =
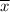`\overline{x}` = 183

Standard deviation of the sample =
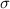`\sigma` = 12

sample size = n = 25

Using t distribution,

`t=\frac{\overline{x}-\mu}{(\sigma)/(√(n))}`

`=(183-160)/((12)/(√(25)))`

`=9.58`

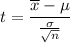
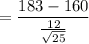
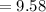
P-value =
`P(t > 9.58)\approx 0`

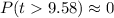
As the obtained value is less than 0.05 or 5% level of significance, so we have to reject the null hypothesis.