Answer: The probability of throwing a dart and hitting the white part of the board is 1.
Explanation:
Since we have given that
Radius of shaded center circle = 1
So, Area of shaded center circle is given by
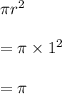
Radius of entire dartboard = 4
Area of entire dartboard is given by
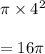
Area of white part is given by
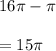
So, Probability of throwing a dart and hitting the white part of the board is given by
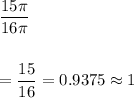
Hence, the probability of throwing a dart and hitting the white part of the board is 1.