Question

The function y = f(x) is graphed below. Plot a line segment connecting the points on f where x = 2 and X 7. Use the line segment to determine the average rate of change of the function f(x) on the interval 2 < x < 7.

Answer 1

You need to start by drawing the line segment that connects the points on the function where x=2 and x=7.

As you can see in the graph, these points are located at:

(2, 10) and (7, -5)

Thus, the line segment will look like:

To determine the average rate of change of the function on the given interval you can use the next formula:

`\text{Average rate of change =}(y1-y2)/(x1-x2)`

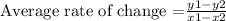
Then, by replacing the coordinates of point 1 and point 2, we obtain:

`\begin{gathered} \text{Average rate of change =}(10-(-5))/(2-7) \\ \text{Average rate of change =}(10+5)/(2-7) \\ \text{Average rate of change =}(15)/(-5) \\ \text{Average rate of change =}-3 \end{gathered}`

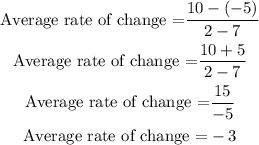
The average rate of change on the interval 2