Question

The table represents a linear function. What is the slope of the function?-10 –5 5 10

Answer 1

the answer would be option 3, which is 5 

Answer 2

Answer: The correct option is (C) 5.

Step-by-step explanation: We are given to find the slope of the linear function represented by the table below:

x -4 -2 0 2 4

y -16 -6 4 14 24

Therefore, the points lying on the straight line represented by the function are

(x, y) = (-4, -16), (-2, -6), (0, 4), (2, 14), (4, 24), etc..

We know that if (a, b) and (c, d) be any two points lying on a straight line, then the slope of the line will be

`s=(d-b)/(c-a).`

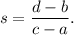
Let,

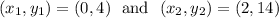`(x_1, y_1)=(0,4)~~\textup{and}~~(x_2,y_2)=(2,14)` be the two points.

Therefore, the slope of the given linear function is

`s=(y_2-y_1)/(x_2-x_1)=(14-4)/(2-0)=(10)/(2)=5.`

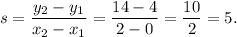
Thus, the slope of the function is .

Option (C) is correct.