Question

A software company sells an education version (e) and a commercial version (c) of its popular image editing software. During the month of January 500 copies of the software are sold with sales totaling $180,000. If the price of the education version is $150 and the price of the commercial version is $600 how many of each version were sold?

Answer 1

150x+600 (500-x)=180000
Solve for x
X=266.66670 education version

500-266.6667=233.3333commercial version

Answer 2

The company sold nearly 267 educational version copies and nearly 233 commercial version copies.

Explanation:

Let the education version software be = e

Let the commercial version software be = c

Equations forms:

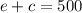`e+c=500` .......(1)

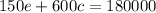`150e+600c=180000` ...... (2)

Multiplying (1) by 150 and subtracting from (2)

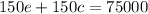`150e+150c=75000` subtracting this from (2)

450c=105000

c = 233.33 rounding to 233

Then
`e=500-233=267`

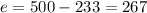
e = 267

Hence, the company sold nearly 267 educational version copies and nearly 233 commercial version copies.