Answer: The correct option is
(B) 74 because ∠TRS and ∠TMN are corresponding angles.
Step-by-step explanation: Given that the line segment RS is parallel to the line segment MN.
We are to find the value of a.
From the figure, we note that
RS is parallel to MN and TM is a transversal.
So, we get
![m\angle TRS=m\angle TMN~~~~~~~~\textup{[corresponding angles]}](https://img.qammunity.org/2018/formulas/mathematics/middle-school/42gkr1mg6xw8kjir9qktphcb15dv1s31dn.png)
Now,
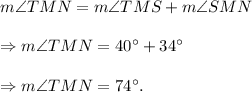
Therefore, we get
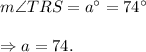
Thus, the value of a is 74, because ∠TRS and ∠TMN are corresponding angles.
Option (B) is correct.