Question

A 0.321-kg mass is attached to a spring with a force constant of 12.3 N/m. If the mass is displaced 0.256 m from equilibrium and released, what is it's speed when it is 0.128 m from equilibrium?

Answer 1

Use the potential energy equation of E = (1/2)kx^2.
If you find the potential energy at both points, you get E = 0.40305J at 0.256m and E = 0.1008J at 0.128m. Subtracting these two you get what potential energy has been lost (E = 0.3023J). Since there is no friction, all of this potential has been turned to kinetic energy E = (1/2)mv^2. Solving this for v I get 1.37237m/s

Answer 2

Speed, v = 1.37 m/s

Step-by-step explanation:

Given that,

Mass of the object, m = 0.321 kg

Force constant, k = 12.3 N/m

Amplitude, A = 0.256 m

Position from equilibrium, x = 0.128 m

To find,

The speed of the object.

Solution,

The velocity of the object that is executing SHM is given by :

`v=\omega√(A^2-x^2)`

`v=\sqrt{(k)/(m)}√(A^2-x^2)`

`v=\sqrt{(12.3)/(0.321)}√(0.256^2-0.128^2)`

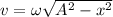
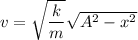
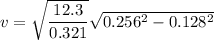
v = 1.37 m/s

So, the speed of the object is 1.37 m/s.