Question

How many positive integers $n$ satisfy $127 \equiv 7 \pmod{n}$? $n=1$ is allowed.

Answer 1

Naturally, any integer
`n` larger than 127 will return
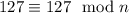
`127\equiv127\mod n`, and of course
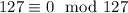
`127\equiv0\mod127`, so we restrict the possible solutions to
`1\le n<127`.

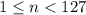
Now,


`127\equiv7\mod n`

is the same as saying there exists some integer
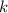
`k` such that


`127=nk+7`

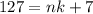
We have


`\implies 120=nk`

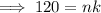
which means that any
`n` that satisfies the modular equivalence must be a divisor of 120, of which there are 16:
`\{1,2,3,4,5,6,8,10,12,15,20,24,30,40,60,120\}`.

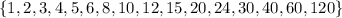
In the cases where the modulus is smaller than the remainder 7, we can see that the equivalence still holds. For instance,


`127=21\cdot6+1\iff127\equiv1\equiv7\mod6`

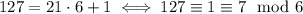
(If we're allowing
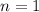
`n=1`, then I see no reason we shouldn't also allow 2, 3, 4, 5, 6.)