Question

Two cars leave the same location traveling in opposite directions. One car leaves at 3:00 p.m. traveling at an average rate of 55 mph. The other car leaves at 4:00 p.m. traveling at an average rate of 75 mph. How many hours after the first car leaves will the two cars be 380 mi apart?

Let x represent the number of hours after the first car leaves.

Enter an equation that can be used to solve this problem in the first box. Solve for x and enter the number of hours in the second box.

Answer 1

55x + 75(x-1) = 380

After 3.5 hours

Explanation:

Two cars leave the same location travelling in opposite directions.

One car leaves at 3:00 p.m. travelling at an average rate of 55 mph.

Other car leaves at 4:00 p.m. travelling at an average rate of 75 mph.

We have to find

Distance traveled by first car + distance traveled by second car = 380 mi

Formula of distance = Speed × time

So the first car travels x hours and the second car travels after one hour so second car travels = x - 1 so the equation will be :

55x + 75(x-1) = 380

55x + 75x - 75 = 380

130x = 455

x =
`(455)/(130)`

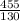
x = 3.5 hours

Therefore, After 3.5 hours the cars will have at a distance of 380 miles.

Answer 2

To answer this item, we let x be the number of hours after 3:00 pm, that the cars will be 380 miles apart. The distance is equal to the product of time and speed. The equation that would best represent the given is,
75(x - 1) - 55x = 380
The value of x from the equation is 22.75 hours.