Question

Find the average rate of change of a function that contains the points (-2,3) and (2,5).

Answer 1

average rate of change is total change in y divided by total change in x...

r=(5-3)/(2--2)

r=2/4

r=1/2

Answer 2

Answer: 0.5

Explanation:

We know that the average rate of change of a function that contains the points (a,b) to (c,d) is given by :-

`(d-b)/(c-a)`

Then, the average rate of change of a function that contains the points (-2,3) and (2,5)will be:-

`(5-3)/(2-(-2))=(2)/(2+2)\\\\=(2)/(4)=0.5`

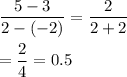
Hence, the average rate of change of a function that contains the points (-2,3) and (2,5). = 0.5