Question

What is the coordinate?

Answer 1

Remember that the equation of a circle is:

`(x - h)^(2) + (y - k)^(2) = r^(2)`
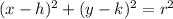
Where (h, k) is the center and r is the radius.
We need to get the equation into that form, and find k.


`x^(2) - 6x + y^(2) - 10y = 56`

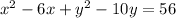
Complete the square. We must do this for x² - 6x and y² - 10y separately.

x² - 6x
Divide -6 by 2 to get -3.
Square -3 to get 9. Add 9,
x² - 6x + 9

Because we've added 9 on one side of the equation, we have to remember to do the same on the other side.


`x^(2) - 6x + 9 + y^(2) - 10y = 65`

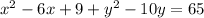
Now factor x² - 6x + 9 to get (x - 3)² and do the same thing with y² - 10y.

y² - 10y
Divide -10 by 2 to get -5.
Square -5 to get 25.
Add 25 on both sides.


`(x - 3)^(2)+ y^(2) - 10y + 25= 90`

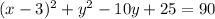
Factor y² - 10y + 25 to get (y - 5)²


`(x - 3)^(2)+ (y - 5)^(2) = 90`

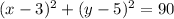
Now our equation is in the correct form. We can easily see that h is 3 and k is 5. (not negative because the original equation has -h and -k so you must multiply -1 to it)

Since (h, k) represents the center, (3, 5) is the center and 5 is the y-coordinate of the center.