Answer:
Option a - 3
Explanation:
Given : Expression
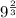
To find :
The value remains under the radical.?
Solution :
We have to solve the expression in simpler form,
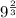
We can re-write as,
![=\sqrt[3]{9^2}](https://img.qammunity.org/2018/formulas/mathematics/high-school/jnse1ka509xwmew9y5385tec2gdqj2ge8z.png)
![=\sqrt[3]{81}](https://img.qammunity.org/2018/formulas/mathematics/high-school/rpav2d3hh0dqilca2d892k38j5md70jw7p.png)
![=\sqrt[3]{3* 3* 3* 3}](https://img.qammunity.org/2018/formulas/mathematics/high-school/7d163xbtxs9sfggt0o1og7x6bnp64bnrha.png)
![=3\sqrt[3]{3}](https://img.qammunity.org/2018/formulas/mathematics/high-school/9ddmcldeo9dix429ump50tf8tb2oc6f60g.png)
Therefore, The value remains under the radical is 3.
Hence, Option a is correct.