Question

Which trigonometric function is equivalent to f(x)=sinx ?

f(x)=cos(x-3pi/2)
f(x)=cos(x-pi/2)
f(x)=cos(-x-pi/2)  <-- i think this one,not sure
f(x)=cos(x+pi)

Answer 1

sin(x) = cos(pi/2 - x)
cos(y) = cos(-y)
sin(x) = cos(x -pi/2)
... look at unit circle , cos is x, sin is y and examine their relations... it's easy to find relation from that .

Answer 2

Answer: The correct option is (B)
`f(x)=\cos\left(x-(\pi)/(2)\right).`

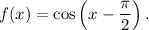
Step-by-step explanation: We are given to select the correct trigonometric function that is equivalent to the following trigonometric function :

`f(x)=\sin x.`

Option (A) :

Here, the given function is

`f(x)\\\\=\cos\left(x-3(\pi)/(2)\right)\\\\=\cos\{-\left(3(\pi)/(2)-x\right)\}\\\\=\cos \left(3(\pi)/(2)-x\right)\\\\=-\sin x\\eq \sin x.`

So, this option is incorrect.

Option (B) :

Here, the given function is

`f(x)\\\\=\cos\left(x-(\pi)/(2)\right)\\\\=\cos\{-\left((\pi)/(2)-x\right)\}\\\\=\cos \left((\pi)/(2)-x\right)\\\\=\sin x.`

So, this option is CORRECT.

Option (C) :

Here, the given function is

`f(x)\\\\=\cos\left(-x-(\pi)/(2)\right)\\\\=\cos\{-\left((\pi)/(2)+x\right)\}\\\\=\cos \left((\pi)/(2)+x\right)\\\\=-\sin x\\eq \sin x.`

So, this option is incorrect.

Option (D) :

Here, the given function is

`f(x)\\\\=\cos\left(x+\pi\right)\\\\=\cos\left(2(\pi)/(2)+x\right)\}\\\\=-\cos x\\eq \sin x.`

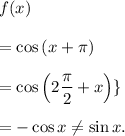
So, this option is incorrect.

Thus, (B) is the correct option.