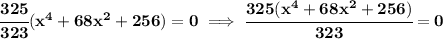Question

Find an n^th degree polynomial with real coefficients satisfying the given conditions. n=4: 2i and -8i are zeros; f(-1)=325 The expanded and simplified polynomial is f(x)=

I had posted a similar question before and followed the steps but I'm doing something wrong and i'm not sure what

Answer 1

as you know, complex roots come with their sister, the conjugate
thus, you have 2i, -2i, -8i, 8i


`\bf \begin{cases} x=2i\implies &x-2i=0\\ x=-2i\implies &x+2i=0\\ x=-8i\implies &x+8i=0\\ x=8i\implies &x-8i=0 \end{cases} \\\\\\ (x-2i)(x+2i)(x+8i)(x-8i)=0\implies [x^2-(2i)^2][x^2-(8i)^2]=0 \\\\\\ (x^2+4)(x^2+64)=0\implies x^4+68x^2+256=0`

now, if we do f(-1), we'd end up with 323, not 325
so.. .what common factor can we stick there to get a 325?

well, let's say hmm "a"
`\bf a(323)=325\implies a=\cfrac{325}{323}`

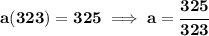
there's our common factor

thus
`\bf \cfrac{325}{323}(x^4+68x^2+256)=0\implies \cfrac{325(x^4+68x^2+256)}{323}=0`