Question

Find an n^th degree polynomial with real coefficients satisfying the given conditions. n = 3; -2 and 2 i are zeros; f(-1) = 15. The expanded and simplified polynomial is f(x) =

Answer 1

so, n = 3, is a 3rd degree polynomial, roots are -2 and 2i

well 2i is a complex root, or imaginary, and complex root never come all by their lonesome, their sister is always with them, the conjugate, so if 0+2i is there, 0-2i is there too

so, the roots are -2, 2i, -2i

now...
`\bf \begin{cases} x=-2\implies x+2=0\implies &(x+2)=0\\ x=2i\implies x-2i=0\implies &(x-2i)=0\\ x=-2i\implies x+2i=0\implies &(x+2i)=0 \end{cases} \\\\\\ (x+2)\underline{(x-2i)(x+2i)}=0\\\\ -----------------------------\\\\ \textit{difference of squares} \\ \quad \\ (a-b)(a+b) = a^2-b^2\qquad \qquad a^2-b^2 = (a-b)(a+b)\\\\ -----------------------------\\\\ (x+2)[x^2-(2i)^2]=0\implies (x+2)[x^2-(2^2i^2)]=0 \\\\\\ (x+2)[x^2-(4\cdot -1)]=0\implies (x+2)(x^2+4)=0 \\\\\\ x^3+2x^2+4x+8=0`

now, if we check f(-1), we end up with 5, not 15
hmmm

so, how to turn our 5 to 15? well, 3*5, thus


`\bf 3(x^3+2x^2+4x+8)=f(x)\implies 3(5)=f(-1)\implies 15=f(-1)`

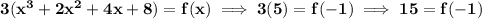
usually, when we get the roots, or zeros, if any common factor that is a constant is about, they get in a division with 0 and get tossed, and aren't part of the roots, thus, we can simply add one, in this case, the common factor of 3, to make the 5 turn to 15