Answer:
The required equation is
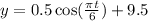 .
.
Explanation:
It is given that the height, h, in feet of the tip of the hour hand of a wall clock varies from 9 feet to 10 feet. It means the minimum height is 9 feet and the maximum height is 10.
At x=0 is 12:00 a.m, it means the function is maximum at x=0. So, the general equation is defined as
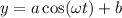
Where, a is amplitude, w is period, t is time in hours and b is midline.
Midline is the average of minimum and maximum height.

Amplitude is the distance of maximum of minimum value from midline.
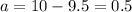
Now, the equation can be written as
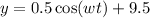 .... (1)
.... (1)
At t = 0 is 12:00 a.m, so t=3 is 3:00 a.m and the y=9.5 at x=3.
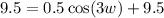
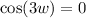
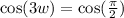
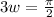

Substitute this value in equation (1).
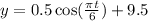
Therefore the required equation is
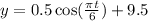 .
.