Answer:
1.

2.
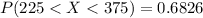
3.

Explanation:
Given information: Population mean = 300 hours, Standard deviation=75
Let X be the life of battery in hours.

(1) The probability that the battery will last less than 250 hours is
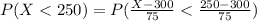
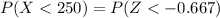

Therefore the probability that the battery will last less than 250 hours is 0.2546.
(2) The probability that the battery will last between 225 and 375 hours is
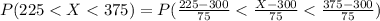
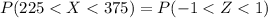
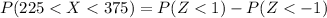
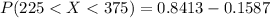
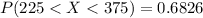
Therefore the probability that the battery will last between 225 and 375 hours is 0.6826.
(3) The probability that the battery will last more than 400 hours is
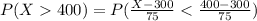
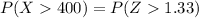
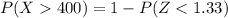


Therefore the probability that the battery will last more than 400 hours is 0.0918.