Question

Please help. How do I solve this?

Answer 1

`\bf \begin{array}{lclll} \underline{2}&\underline{-2} i\\ a&b \end{array}\qquad \begin{cases} r=√(a^2+b^2)\\\\ \theta=tan^(-1)\left( (b)/(a) \right) \end{cases}\\\\ -----------------------------\\\\ r=√(2^2+(-2)^2)\implies r=√(8)\implies r=2√(2) \\\\\\ \theta=tan^(-1)\left( \cfrac{-2}{2} \right)\implies \theta=tan^(-1)(-1)\qquad \theta= \begin{cases} (3\pi )/(4)\\\\ (7\pi )/(4) \end{cases}`

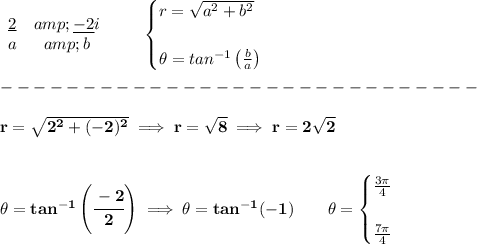
so, either of those angles, have a tangent of -1, check your Unit Circle

however, notice the rectangular is 2 and -2i, or 2,-2i, that's on the 4th quadrant, graph it and check, so, the angle for that rectangular will the be
`\bf (7\pi )/(4)`

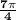
now, the polar form of any rectangular is
`\bf r[cos(\theta)-i\ sin(\theta)]`

thus
`\bf 2,-2i\implies 2√(2)\left[ cos\left( (7\pi )/(4) \right) +i\ sin\left( (7\pi )/(4) \right)\right]`