Answer:
Triangle ABC is isosceles.
Explanation:
An isosceles triangle means two sides of the triangle should be equal.
Given vertices of the triangle are A(0, 2), B(2, 5) and C(-1, 7)
We will use the formula to find the length
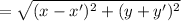
Now length AB =
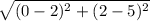
=
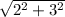
=
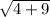
=
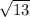
Length AV =
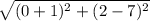
=
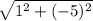
=
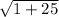
=
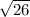
Length BC =
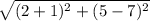
=
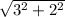
=
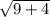
=
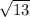
mAB = mBC =
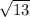 ,
,
Therefore, triangle ABC is isosceles.