Answer:
The average rate of change is -158 feet per second.
Explanation:
Given : A ball is thrown upward from the top of a building. The function below shows the height of the ball in relation to sea level, f(t), in feet, at different times, t, in seconds :
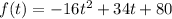
To find : The average rate of change of f(t) from t = 5 seconds to t = 7 seconds ?
Solution :
First we find the value of f(t) at t=5 and t=7
At t=5 seconds
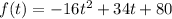

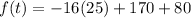
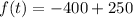
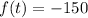
At t=7 seconds
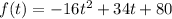
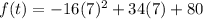
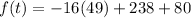

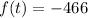
The average rate of change is
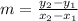
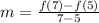
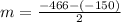
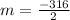
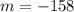
Therefore, The average rate of change is -158 feet per second.