Question

Which function grows at the fastest rate for increasing values of x?

f(x)=9x+14

g(x)=4x

h(x)=6x^2+1

Answer 1

take derivitive of each

f'(x)=9
g'(x)=4
h'(x)=12x

so duh, when x>0.75 then h(x) grows at fastest rate, after that. it just keeps going up

Answer 2

`\text{Exponential Function: }g(x)=4^x`

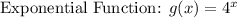
B is correct.

Step-by-step explanation:

Given:

`\text{Linear Function: }f(x)=9x+14`

`\text{Exponential Function: }g(x)=4^x`

`\text{Quadratic Function: }h(x)=6x^2+1`

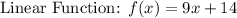
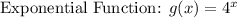
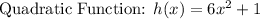
All the functions are specific function.

Growth rate of these function. ( If all are in same increasing )

Exponential > Quadratic > Linear

For increasing value of x

All three functions are increasing function.

Please see the attachment for graph for grow.

Hence, Exponential function grow fastest rate for increasing value of x is g(x)=4ˣ