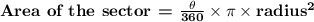Question

The area of a circle is πr2. To find the area of a sector with a central angle of Θ, measured in radians, by what should you multiply πr2?

Answer 1

there are 2pi radians in a circle

so the fraciton is Θ/(2pi)

so
pir^2 times Θ/(2pi)=pir^2Θ/2pi=Θr^2/2
multiply it by Θ/(2pi)

Answer 2

`\bf\textbf{Area of the sector = }(\theta)/(360)* \pi* radius^2`

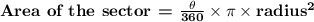
Explanation:

`\text{The area of the circle is }\pi* radius^2`

Now, To find the area of the sector of the circle we must be given the value of the central angle.

In this case, The central angle of the circle is given to be Θ

Now, The measure of one complete angle is 360

So, to find the area of the sector we need to divide the central angle Θ by 360

Hence, the resultant area of the sector of the circle is given by the formula :

`\bf\textbf{Area of the sector = }(\theta)/(360)* \pi* radius^2`