Question

The equation of a circle in general form is ​ x2+y2+18x−36y+369=0 ​

What is the equation of the circle in standard form?

Answer 1

You have to complete the square of (x²+18x+?) as well as for (y²-36y+?)

You will find: (x+9)² + (y-18)² = 36


& this is the standard equation requested

Answer 2

`(x+9)^2+(y-18)^2=6^2`

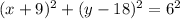
Explanation:

We have been given equation of a circle in general form
`x^2+y^2+18x-36y+369=0`. We are asked to find the equation of the circle in standard form.

We know that equation of a circle in standard form is of format:
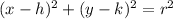`(x-h)^2+(y-k)^2=r^2`, where (h,k) represents the center of the circle and r represents radius.

We will convert our given equation in standard form by completing the squares as shown below:

`x^2+18x+y^2-36y+369-369=0-369`

`x^2+18x+y^2-36y=-369`

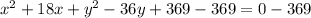
Adding
`((b)/(2))^2` to both sides of our equation we will get,

`((18)/(2))^2=(9)^2=81`

`((36)/(2))^2=(18)^2=324`

`x^2+18x+81+y^2-36y+324=-369+81+324`

`x^2+18x+81+y^2-36y+324=36`

`(x+9)^2+(y-18)^2=6^2`

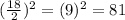
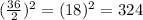
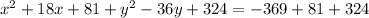
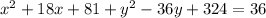
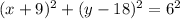
Therefore, the equation of the given circle in standard form would be
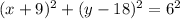`(x+9)^2+(y-18)^2=6^2`.